Fifth Competition following Youhan Lee's curriculum. Multi-class classification competition using tabular data.
Costa Rican Household Poverty Level Prediction
Can you identify which households have the highest need for social welfare assistance?
www.kaggle.com
First Kernel: A Complete Introduction and Walkthrough
- Overall walkthrough on the competition: from eda to modeling.
Insight / Summary:
1. Metric
- Ultimately we want to build a machine learning model that can predict the integer poverty level of a household.
- Our predictions will be assessed by the Macro F1 Score.
- You may be familiar with the standard F1 score for binary classification problems which is the harmonic mean of precision and recall:
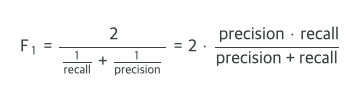
- For mutli-class problems, we have to average the F1 scores for each class.
- The macro F1 score averages the F1 score for each class without taking into account label imbalances.

- In other words, the number of occurrences of each label does not figure into the calculation when using macro (while it does when using the "weighted" score).
- If we want to assess our performance, we can use the code:
from sklearn.metrics import f1_score
f1_score(y_true, y_predicted, average = 'macro`)- For this problem, the labels are imbalanced, which makes it a little strange to use macro averaging for the evaluation metric, but that's a decision made by the organizers and not something we can change!
- In your own work, you want to be aware of label imbalances and choose a metric accordingly.
2. Plotting float values
- Float column type represent continuous variables.
- When making distribution plot to show the distribution of all float columns, we can use an OrderedDict to map the poverty levels to colors because this keeps the keys and values in the same order as we specify (unlike a regular Python dictionary).
- The following graphs shows the distributions of the float columns colored by the value of the Target.
- With these plots, we can see if there is a significant difference in the variable distribution depending on the household poverty level.
from collections import OrderedDict
plt.figure(figsize = (20, 16))
plt.style.use('fivethirtyeight')
# Color mapping
colors = OrderedDict({1: 'red', 2: 'orange', 3: 'blue', 4: 'green'})
poverty_mapping = OrderedDict({1: 'extreme', 2: 'moderate', 3: 'vulnerable', 4: 'non vulnerable'})
# Iterate through the float columns
for i, col in enumerate(train.select_dtypes('float')):
ax = plt.subplot(4, 2, i + 1)
# Iterate through the poverty levels
for poverty_level, color in colors.items():
# Plot each poverty level as a separate line
sns.kdeplot(train.loc[train['Target'] == poverty_level, col].dropna(),
ax = ax, color = color, label = poverty_mapping[poverty_level])
plt.title(f'{col.capitalize()} Distribution'); plt.xlabel(f'{col}'); plt.ylabel('Density')
plt.subplots_adjust(top = 2)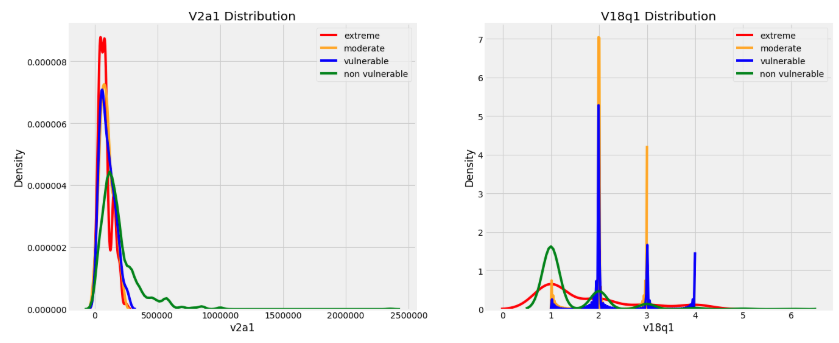
3. Addressing Wrong Labels
- As with any realistic dataset, the Costa Rican Poverty data has some issues.
- Typically, 80% of a data science project will be spent cleaning data and fixing anomalies/errors.
- These can be either human entry errors, measurement errors, or sometimes just extreme values that are correct but stand out.
- For this problem, some of the labels are not correct because individuals in the same household have a different poverty level.
- We're not told why this may be the case, but we are told to use the head of household as the true label.
- That information makes our job much easier, but in a real-world problem, we would have to figure out the reason Why the labels are wrong and how to address the issue on our own.
- This section fixes the issue with the labels although it is not strictly necessary: I kept it in the notebook just to show how we may deal with this issue.
1) Identify Errors
- First we need to find the errors before we can correct them.
- To find the households with different labels for family members, we can group the data by the household and then check if there is only one unique value of the Target.
# Groupby the household and figure out the number of unique values
all_equal = train.groupby('idhogar')['Target'].apply(lambda x: x.nunique() == 1)
# Households where targets are not all equal
not_equal = all_equal[all_equal != True]
print('There are {} households where the family members do not all have the same target.'.format(len(not_equal)))
# result: There are 85 households where the family members do not all have the same target.- The organizers tell us that the correct label is that for the head of household, where parentesco1 == 1.
- We can correct this by reassigning all the individuals in this household the correct poverty level.
- In the real-world, you might have to make the tough decision of how to address the problem by yourself (or with the help of your team).
2) Families without Heads of Household
- We can correct all the label discrepancies by assigning the individuals in the same household the label of the head of household.
- But wait, you may ask: "What if there are households without a head of household? And what if the members of those households have differing values of the label?"
households_leader = train.groupby('idhogar')['parentesco1'].sum()
# Find households without a head
households_no_head = train.loc[train['idhogar'].isin(households_leader[households_leader == 0].index), :]
print('There are {} households without a head.'.format(households_no_head['idhogar'].nunique()))
# result: There are 15 households without a head.# Find households without a head and where labels are different
households_no_head_equal = households_no_head.groupby('idhogar')['Target'].apply(lambda x: x.nunique() == 1)
print('{} Households with no head have different labels.'.format(sum(households_no_head_equal == False)))
# result: 0 Households with no head have different labels.- This means that we don't have to worry about a household both where there is no head AND the members have different values of the label
- For this problem, according to the organizers, if a household does not have a head, then there is no true label.
- Therefore, we actually won't use any of the households without a head for training
3) Correct Errors
- Now we can correct labels for the households that do have a head AND the members have different poverty levels.
# Iterate through each household
for household in not_equal.index:
# Find the correct label (for the head of household)
true_target = int(train[(train['idhogar'] == household) & (train['parentesco1'] == 1.0)]['Target'])
# Set the correct label for all members in the household
train.loc[train['idhogar'] == household, 'Target'] = true_target
# Groupby the household and figure out the number of unique values
all_equal = train.groupby('idhogar')['Target'].apply(lambda x: x.nunique() == 1)
# Households where targets are not all equal
not_equal = all_equal[all_equal != True]
print('There are {} households where the family members do not all have the same target.'.format(len(not_equal)))
# result: There are 0 households where the family members do not all have the same target.- Since we are only going to use the heads of household for the labels, this step is not completely necessary but it shows a workflow for correcting data errors like you may encounter in real life.
4. Measuring Relationships
- There are many ways for measuring relationships between two variables.
- Here we will examine two of these:
- The Pearson Correlation: from -1 to 1 measuring the linear relationship between two variables
- The Spearman Correlation: from -1 to 1 measuring the monotonic relationship between two variables
- The Spearman correlation is 1 if as one variable increases, the other does as well, even if the relationship is not linear.
- On the other hand, the Pearson correlation can only be one if the increase is exactly linear.
- The Spearman correlation is often considered to be better for ordinal variables such as the Target or the years of education.
- Most relationship in the real world aren't linear, and although the Pearson correlation can be an approximation of how related two variables are, it's inexact and not the best method of comparison.
5. Spearman correlation applied
import warnings
warnings.filterwarnings('ignore', category = RuntimeWarning)
feats = []
scorr = []
pvalues = []
# Iterate through each column
for c in heads:
# Only valid for numbers
if heads[c].dtype != 'object':
feats.append(c)
# Calculate spearman correlation
scorr.append(spearmanr(train_heads[c], train_heads['Target']).correlation)
pvalues.append(spearmanr(train_heads[c], train_heads['Target']).pvalue)
scorrs = pd.DataFrame({'feature': feats, 'scorr': scorr, 'pvalue': pvalues}).sort_values('scorr')- The Spearman correlation coefficient calculation also comes with a pvalue indicating the significance level of the relationship.
- Any pvalue less than 0.05 is genearally regarded as significant, although since we are doing multiple comparisons, we want to divide the p-value by the number of comparisons, a process known as the Bonferroni correction.
6. Jitter
- "Jitter" is an important technique used in data visualization.
- It means intentionally adding small random noise (random variation) to data points.
- The main purposes are:
- Solving overlapping data points problem
- Especially with discrete data, many points can overlap at exactly the same position
- Adding jitter helps avoid this overlap and better shows the distribution of data
- Improving visual clarity
- Better shows the density and distribution of data
- Allows distinguishing between overlapping points
- Solving overlapping data points problem
- For example:
- If you have survey data with scores only from 1, 2, 3, 4, 5
- Without jitter, many points would overlap exactly at these five values
- With jitter, points are slightly scattered around each score, making it easier to see the actual patterns in the data
- In this case, since both Target and dependency are discrete variables, adding jitter can help visualize the relationship between the two variables more clearly.
7. Plotting feature importance code sample that can be reused
def plot_feature_importances(df, n = 10, threshold = None):
"""Plots n most important features. Also plots the cumulative importance if
threshold is specified and prints the number of features needed to reach threshold cumulative importance.
Intended for use with any tree-based feature importances.
Args:
df (dataframe): Dataframe of feature importances. Columns must be "feature" and "importance".
n (int): Number of most important features to plot. Default is 15.
threshold (float): Threshold for cumulative importance plot. If not provided, no plot is made. Default is None.
Returns:
df (dataframe): Dataframe ordered by feature importances with a normalized column (sums to 1)
and a cumulative importance column
Note:
* Normalization in this case means sums to 1.
* Cumulative importance is calculated by summing features from most to least important
* A threshold of 0.9 will show the most important features needed to reach 90% of cumulative importance
"""
plt.style.use('fivethirtyeight')
# Sort features with most important at the head
df = df.sort_values('importance', ascending = False).reset_index(drop = True)
# Normalize the feature importances to add up to one and calculate cumulative importance
df['importance_normalized'] = df['importance'] / df['importance'].sum()
df['cumulative_importance'] = np.cumsum(df['importance_normalized'])
plt.rcParams['font.size'] = 12
# Bar plot of n most important features
df.loc[:n, :].plot.barh(y = 'importance_normalized',
x = 'feature', color = 'darkgreen',
edgecolor = 'k', figsize = (12, 8),
legend = False, linewidth = 2)
plt.xlabel('Normalized Importance', size = 18); plt.ylabel('');
plt.title(f'{n} Most Important Features', size = 18)
plt.gca().invert_yaxis()
if threshold:
# Cumulative importance plot
plt.figure(figsize = (8, 6))
plt.plot(list(range(len(df))), df['cumulative_importance'], 'b-')
plt.xlabel('Number of Features', size = 16); plt.ylabel('Cumulative Importance', size = 16);
plt.title('Cumulative Feature Importance', size = 18);
# Number of features needed for threshold cumulative importance
# This is the index (will need to add 1 for the actual number)
importance_index = np.min(np.where(df['cumulative_importance'] > threshold))
# Add vertical line to plot
plt.vlines(importance_index + 1, ymin = 0, ymax = 1.05, linestyles = '--', colors = 'red')
plt.show();
print('{} features required for {:.0f}% of cumulative importance.'.format(importance_index + 1,
100 * threshold))
return df
8.

- The graph below (from the paper by Randal Olson) shows the effect of hyperparameter tuning versus the default values in Scikit-Learn.
- In most cases the accuracy gain is less than 10% so the worst model is probably not suddenly going to become the best model through tuning.
9. Recursive Feature Elimination with Random Forest
- The RFECV in Sklearn stands for Recursive Feature Elimination with Cross Validation.
- The selector operates using a model with feature importances in an iterative manner.
- At each iteration, it removes either a fraction of features or a set number of features.
- The iterations continue until the cross validation score no longer improves.
- To create the selector object, we pass in the the model, the number of features to remove at each iteration, the cross validation folds, our custom scorer, and any other parameters to guide the selection.
from sklearn.feature_selection import RFECV
# Create a model for feature selection
estimator = RandomForestClassifier(random_state = 10, n_estimators = 100, n_jobs = -1)
# Create the object
selector = RFECV(estimator, step = 1, cv = 3, scoring= scorer, n_jobs = -1)- Then we fit the selector on the training data as with any other sklearn model.
- This will continue the feature selection until the cross validation scores no longer improve.
selector.fit(train_set, train_labels)
# result: RFECV(cv=3,
# estimator=RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
# max_depth=None, max_features='auto', max_leaf_nodes=None,
# min_impurity_decrease=0.0, min_impurity_split=None,
# min_samples_leaf=1, min_samples_split=2,
# min_weight_fraction_leaf=0.0, n_estimators=100, n_jobs=-1,
# oob_score=False, random_state=10, verbose=0, warm_start=False),
# min_features_to_select=1, n_jobs=-1,
# scoring=make_scorer(f1_score, average=macro), step=1, verbose=0)train_selected = selector.transform(train_set)
test_selected = selector.transform(test_set)
10.
- The predicted distribution looks close to the training distribution although there are some differences.
- Depending on the run of the notebook, the results you see may change, but for this edition, the 4s are underrepresented in the predictions and the 3s are overrepresented.
- One potentially method for dealing with imbalanced classification problems is oversampling the minority class, which is easy to do in Python using the imbalanced learn library.
11. Validation
- For the test predictions, we can only compare the distribution with that found on the training data.
- If we want to compare predictions to actual answers, we'll have to split the training data into a separate validation set.
- We'll use 1000 examples for testing and then we can do operations like make the confusion matrix because we have the right answer.
Confusion matrix code:
from sklearn.metrics import confusion_matrix
import itertools
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Oranges):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
Source: http://scikit-learn.org/stable/auto_examples/model_selection/plot_confusion_matrix.html
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.figure(figsize = (10, 10))
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title, size = 24)
plt.colorbar(aspect=4)
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45, size = 14)
plt.yticks(tick_marks, classes, size = 14)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
# Labeling the plot
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt), fontsize = 20,
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.grid(None)
plt.tight_layout()
plt.ylabel('True label', size = 18)
plt.xlabel('Predicted label', size = 18)
12.
- Overall, these results show that imbalanced classification problems with relatively few observations are very difficult.
- There are some methods we can take to try and counter this such as oversampling or training multiple models on different sections of the data, but at the end of the day, the most effective method may be to gather more data.
13. Dimension Reduction
- As a final exploration of the problem, we can apply a few different dimension reductions methods to the selected data set.
- These methods can be used for visualization or as a preprocessing method for machine learning.
- Four different methods:
- PCA: Principal Components Analysis. Finds the dimensions of greatest variation in the data
- ICA: Independent Components Analysis. Attempts to separate a mutltivariate signal into independent signals.
- TSNE: T-distributed Stochastic Neighbor Embedding. Maps high-dimensional data to a low-dimensional manifold attempting to maintain the local structure within the data. It is a non-linear technique and generally only used for visualization.
- UMAP: Uniform Manifold Approximation and Projection: A relatively new technique that also maps data to a low-dimensional manifold but tries to preserve more global structure than TSNE.
- All four of these methods are relatively simple to implement in Python.
Second Kernel: 3250feats->532 feats using shap[LB: 0.436]
- Mainly about
Insight / Summary:
1. Checking null data
total = df_train.isnull().sum().sort_values(ascending=False)
percent = 100 * (df_train.isnull().sum() / df_train.isnull().count()).sort_values(ascending=False)
missing_df = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_df.head(20)
2. Feature selection using shap
binary_cat_features = [col for col in train.columns if train[col].value_counts().shape[0] == 2]
object_features = ['edjefe', 'edjefa']
categorical_feats = binary_cat_features + object_featuresdef evaluate_macroF1_lgb(truth, predictions):
# this follows the discussion in https://github.com/Microsoft/LightGBM/issues/1483
pred_labels = predictions.reshape(len(np.unique(truth)),-1).argmax(axis=0)
f1 = f1_score(truth, pred_labels, average='macro')
return ('macroF1', f1, True)y = train['Target']
train.drop(columns=['Target'], inplace=True)def print_execution_time(start):
end = time.time()
hours, rem = divmod(end-start, 3600)
minutes, seconds = divmod(rem, 60)
print('*'*20, "Execution ended in {:0>2}h {:0>2}m {:05.2f}s".format(int(hours),int(minutes),seconds), '*'*20)def extract_good_features_using_shap_LGB(params, SEED):
clf = lgb.LGBMClassifier(objective='multiclass',
random_state=1989,
max_depth=params['max_depth'],
learning_rate=params['learning_rate'],
silent=True,
metric='multi_logloss',
n_jobs=-1, n_estimators=10000,
class_weight='balanced',
colsample_bytree = params['colsample_bytree'],
min_split_gain= params['min_split_gain'],
bagging_freq = params['bagging_freq'],
min_child_weight=params['min_child_weight'],
num_leaves = params['num_leaves'],
subsample = params['subsample'],
reg_alpha= params['reg_alpha'],
reg_lambda= params['reg_lambda'],
num_class=len(np.unique(y)),
bagging_seed=SEED,
seed=SEED,
)
kfold = 5
kf = StratifiedKFold(n_splits=kfold, shuffle=True)
feat_importance_df = pd.DataFrame()
for i, (train_index, test_index) in enumerate(kf.split(train, y)):
print('='*30, '{} of {} folds'.format(i+1, kfold), '='*30)
start = time.time()
X_train, X_val = train.iloc[train_index], train.iloc[test_index]
y_train, y_val = y.iloc[train_index], y.iloc[test_index]
clf.fit(X_train, y_train, eval_set=[(X_train, y_train), (X_val, y_val)], eval_metric=evaluate_macroF1_lgb, categorical_feature=categorical_feats,
early_stopping_rounds=500, verbose=500)
shap_values = shap.TreeExplainer(clf.booster_).shap_values(X_train)
fold_importance_df = pd.DataFrame()
fold_importance_df['feature'] = X_train.columns
fold_importance_df['shap_values'] = abs(np.array(shap_values)[:, :].mean(1).mean(0))
fold_importance_df['feat_imp'] = clf.feature_importances_
feat_importance_df = pd.concat([feat_importance_df, fold_importance_df])
print_execution_time(start)
feat_importance_df_shap = feat_importance_df.groupby('feature').mean().sort_values('shap_values', ascending=False).reset_index()
# feat_importance_df_shap['shap_cumsum'] = feat_importance_df_shap['shap_values'].cumsum() / feat_importance_df_shap['shap_values'].sum()
# good_features = feat_importance_df_shap.loc[feat_importance_df_shap['shap_cumsum'] < 0.999].feature
return feat_importance_df_shaptotal_shap_df = pd.DataFrame()
NUM_ITERATIONS = 50
for SEED in range(NUM_ITERATIONS):
print('#'*40, '{} of {} iterations'.format(SEED+1, NUM_ITERATIONS), '#' * 40)
params = {'max_depth': np.random.choice([5, 6, 7, 8, 10, 12, -1]),
'learning_rate': np.random.rand() * 0.02,
'colsample_bytree': np.random.rand() * (1 - 0.5) + 0.5,
'subsample': np.random.rand() * (1 - 0.5) + 0.5,
'min_split_gain': np.random.rand() * 0.2,
'num_leaves': np.random.choice([32, 48, 64]),
'reg_alpha': np.random.rand() * 2,
'reg_lambda': np.random.rand() *2,
'bagging_freq': np.random.randint(4) +1,
'min_child_weight': np.random.randint(100) + 20
}
temp_shap_df = extract_good_features_using_shap_LGB(params, SEED)
total_shap_df = pd.concat([total_shap_df, temp_shap_df])Third Kernel: XGBoost
- Mainly about converting lgbm into XGBoost and more.
Insight / Summary:
1.
- It seems to be very important to balance class frequencies.
- Without balancing a trained model gives ~0.39 PLB / ~0.43 local test, while adding balancing leads to ~0.42 PLB / 0.47 local test.
- One can do it by hand, one can achieve it by undersampling.
- But the simplest (and more powerful compared to undersampling) is to set class_weight='balanced' in the LightGBM model constructor in sklearn API.
2.
- OHE if reversed into label encoding, as it is easier to digest for a tree model.
- This trick would be harmful for non-tree models, so be careful.
3. Splitting data
- We split the data by household to avoid leakage, since rows belonging to the same household usually have the same target.
- Since we filter the data to only include heads of household this isn't technically necessary, but it provides an easy way to use the entire training data set if we want to do that.
- Note that after splitting the data we overwrite the train data with the entire data set so we can train on all of the data.
- The split_data function does the same thing without overwriting the data, and is used within the training loop to (hopefully) approximate a K-Fold split.
def split_data(train, y, sample_weight=None, households=None, test_percentage=0.20, seed=None):
# uncomment for extra randomness
# np.random.seed(seed=seed)
train2 = train.copy()
# pick some random households to use for the test data
cv_hhs = np.random.choice(households, size=int(len(households) * test_percentage), replace=False)
# select households which are in the random selection
cv_idx = np.isin(households, cv_hhs)
X_test = train2[cv_idx]
y_test = y[cv_idx]
X_train = train2[~cv_idx]
y_train = y[~cv_idx]
if sample_weight is not None:
y_train_weights = sample_weight[~cv_idx]
return X_train, y_train, X_test, y_test, y_train_weights
return X_train, y_train, X_test, y_testX = train.query('parentesco1==1')
# X = train.copy()
# pull out and drop the target variable
y = X['Target'] - 1
X = X.drop(['Target'], axis=1)
np.random.seed(seed=None)
train2 = X.copy()
train_hhs = train2.idhogar
households = train2.idhogar.unique()
cv_hhs = np.random.choice(households, size=int(len(households) * 0.15), replace=False)
cv_idx = np.isin(train2.idhogar, cv_hhs)
X_test = train2[cv_idx]
y_test = y[cv_idx]
X_train = train2[~cv_idx]
y_train = y[~cv_idx]
# train on entire dataset
X_train = train2
y_train = y
train_households = X_train.idhogarDetailed process explanation:
1) Original Data Structure
data = {
'household_id': [1, 1, 1, 2, 2, 3],
'member_type': ['H', 'W', 'C', 'H', 'W', 'H'], # H:Householder, W:Wife, C:Child
'income': [5000, 3000, 0, 4500, 2800, 3800],
'target': [1, 1, 1, 0, 0, 1] # Same target for each household
}
2) Data Split Process:
A) First, split correctly by household unit:
# Correct method: split by household
train_data = [
# All data from Household 1
(1, 'H', 5000, 1),
(1, 'W', 3000, 1),
(1, 'C', 0, 1),
# All data from Household 2
(2, 'H', 4500, 0),
(2, 'W', 2800, 0)
]
test_data = [
# All data from Household 3
(3, 'H', 3800, 1)
]
B) Then, overwrite train_data with full data for final model training:
# Overwrite - include data from all households
train_data = [
# Household 1
(1, 'H', 5000, 1),
(1, 'W', 3000, 1),
(1, 'C', 0, 1),
# Household 2
(2, 'H', 4500, 0),
(2, 'W', 2800, 0),
# Including Household 3
(3, 'H', 3800, 1)
]
3) Currently using only householder data in the project:
heads_only_data = [
(1, 'H', 5000, 1), # Household 1 householder
(2, 'H', 4500, 0), # Household 2 householder
(3, 'H', 3800, 1) # Household 3 householder
]
Don't be afraid to dream big. The size of your dreams should match the size of your ambition.
- Max Holloway -
'캐글' 카테고리의 다른 글
| [Kaggle Study] #9 New York City Taxi Trip Duration (0) | 2024.11.29 |
|---|---|
| [Kaggle Study] #8 2018 Data Science Bowl (0) | 2024.11.28 |
| [Kaggle Study] #7 TensorFlow Speech Recognition Challenge (0) | 2024.11.27 |
| [Kaggle Study] #4 More about Home Credit Default Risk Competition (0) | 2024.11.26 |
| [Kaggle Study] #5 Statoil/C-CORE Iceberg Classifier Challenge (0) | 2024.11.25 |