Tenth competition following Youhan Lee's curriculum. Anomaly detection competition using tabular data.
Credit Card Fraud Detection
Anonymized credit card transactions labeled as fraudulent or genuine
www.kaggle.com
First Kernel: In depth skewed data classif. (93% recall acc now)
- Testing different methods on skewed data.
- The idea is to compare if preprocessing techniques work better when there is an overwhelming majority class that can disrupt the efficiency of our predictive model.
Insight / Summary:
1. Methodologies for dealing with unbalanced data

- There are several ways to approach this classification problem taking into consideration this unbalance.
- Collect more data? Nice strategy but not applicable in this case
- Changing the performance metric:
- Use the confusion matrix to calculate Precision, Recall
- F1score (weighted average of precision recall)
- Use Kappa - which is a classification accuracy normalized by the imbalance of the classes in the data
- ROC curves - calculates sensitivity/specificity ratio.
- Resampling the dataset
- Essentially this is a method that will process the data to have an approximate 50-50 ratio.
- One way to achieve this is by OVER-sampling, which is adding copies of the under-represented class (better when you have little data)
- Another is UNDER-sampling, which deletes instances from the over-represented class (better when he have lot's of data)
2. Nice approach that can be applied to other anomaly detection problems as well
Approach
- We are not going to perform feature engineering in first instance. The dataset has been downgraded in order to contain 30 features (28 anonymized + time + amount).
- This means that the 28 features in the dataset have been anonymized so that their actual names and meanings cannot be known.
- For example, if the original feature names were "age," "gender," "occupation," etc., they have been changed to neutral names like "V1," "V2," "V3," and so on.
- We will then compare what happens when using resampling and when not using it. We will test this approach using a simple logistic regression classifier.
- When the result is happy with the resampling dataset, we will then apply the same hyperparameter to the whole dataset.
- We will evaluate the models by using some of the performance metrics mentioned above.
- We will repeat the best resampling/not resampling method, by tuning the parameters in the logistic regression classifier.
- We will finally perform classifications model using other classification algorithms.(actually not in this kernel)
3. Resampling process
- As we mentioned earlier, there are several ways to resample skewed data.
- Apart from under and over sampling, there is a very popular approach called SMOTE (Synthetic Minority Over-Sampling Technique), which is a combination of oversampling and undersampling, but the oversampling approach is not by replicating minority class but constructing new minority class data instance via an algorithm.
- In this notebook, we will use traditional UNDER-sampling.
- The way we will under sample the dataset will be by creating a 50/50 ratio.
- This will be done by randomly selecting "x" amount of sample from the majority class, being "x" the total number of records with the minority class.
X = data.ix[:, data.columns != 'Class']
y = data.ix[:, data.columns == 'Class']# Number of data points in the minority class
number_records_fraud = len(data[data.Class == 1])
fraud_indices = np.array(data[data.Class == 1].index)
# Picking the indices of the normal classes
normal_indices = data[data.Class == 0].index
# Out of the indices we picked, randomly select "x" number (number_records_fraud)
random_normal_indices = np.random.choice(normal_indices, number_records_fraud, replace = False)
random_normal_indices = np.array(random_normal_indices)
# Appending the 2 indices
under_sample_indices = np.concatenate([fraud_indices,random_normal_indices])
# Under sample dataset
under_sample_data = data.iloc[under_sample_indices,:]
X_undersample = under_sample_data.ix[:, under_sample_data.columns != 'Class']
y_undersample = under_sample_data.ix[:, under_sample_data.columns == 'Class']
# Showing ratio
print("Percentage of normal transactions: ", len(under_sample_data[under_sample_data.Class == 0])/len(under_sample_data))
print("Percentage of fraud transactions: ", len(under_sample_data[under_sample_data.Class == 1])/len(under_sample_data))
print("Total number of transactions in resampled data: ", len(under_sample_data))Result:
Percentage of normal transactions: 0.5
Percentage of fraud transactions: 0.5
Total number of transactions in resampled data: 984
4. Recall Metric
- We are very interested in the recall score, because that is the metric that will help us try to capture the most fraudulent transactions.
- If you think how Accuracy, Precision and Recall work for a confusion matrix, recall would be the most interesting:
- Accuracy = (TP+TN)/total
- Precision = TP/(TP+FP)
- Recall = TP/(TP+FN)
- As we know, due to the imbalacing of the data, many observations could be predicted as False Negatives, being, that we predict a normal transaction, but it is in fact a fraudulent one. Recall captures this.
- Obviously, trying to increase recall, tends to come with a decrease of precision.
- However, in our case, if we predict that a transaction is fraudulent and turns out not to be, is not a massive problem compared to the opposite.
- Misclassifying a fraudulent transaction as legitimate (False Negative) is a bigger problem
- Than misclassifying a legitimate transaction as fraudulent (False Positive)
- We could even apply a cost function when having FN and FP with different weights for each type of error, but let's leave that aside for now.
5. Result checking process

- The model is offering an 93.2% recall accuracy on the generalised unseen data (test set).
- Not a bad percentage to be the first try.
- However, recall this is a 93.2% recall accuracy measure on the undersampled test set.
- Being happy with this result, let's apply the model we fitted and test it on the whole data.

- Still a very decent recall accuracy when applying it to a much larger and skewed dataset.
- So, we now move on to checking various metrics to evaluate the performance.
6. Plotting ROC curve and Precision-Recall curve
- Found precision-recall curve much more convenient in this case as our problems relies on the "positive" class being more interesting than the negative class, but as we have calculated the recall precision, I am not going to plot the precision recall curves yet.
- AUC and ROC curve are also interesting to check if the model is also predicting as a whole correctly and not making many errors
# ROC CURVE
lr = LogisticRegression(C = best_c, penalty = 'l1')
y_pred_undersample_score = lr.fit(X_train_undersample,y_train_undersample.values.ravel()).decision_function(X_test_undersample.values)
fpr, tpr, thresholds = roc_curve(y_test_undersample.values.ravel(),y_pred_undersample_score)
roc_auc = auc(fpr,tpr)
# Plot ROC
plt.title('Receiver Operating Characteristic')
plt.plot(fpr, tpr, 'b',label='AUC = %0.2f'% roc_auc)
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],'r--')
plt.xlim([-0.1,1.0])
plt.ylim([-0.1,1.01])
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()
- An additional comment that would be interesting to do is to initialize multiple undersampled datasets and repeat the process in loop.
- Remember that, to create an undersample data, we randomly got records from the majority class.
- Even though this is a valid technique, is doesn't represent the real population, so it would be interesting to repeat the process with different undersample configurations and check if the previous chosen parameters are still the most effective.
- In the end, the idea is to use a wider random representation of the whole dataset and rely on the averaged best parameters.
7. Now testing on skewed data after resampled data
- Having tested our previous approach, I find really interesting to test the same process on the skewed data.
- Our intuition is that skewness will introduce issues difficult to capture, and therefore, provide a less effective algorithm.
- To be fair, taking into account the fact that the train and test datasets are substantially bigger than the undersampled ones, I believe a K-fold cross validation is necessary.
- I guess that by splitting the data with 60% in training set, 20% cross validation and 20% test should be enough... but let's take the same approach as before (no harm on this, it's just that K-fold is computationally more expensive)

- Therefore by undersampling the data, our algorithm does a much better job at detecting fraud.
8. Threshold Tuning
- I wanted also to show how can we tweak our final classification by changing the thresold.
- Initially, you build the classification model and then you predict unseen data using it.
- We previously used the "predict()" method to decided whether a record should belong to "1" or "0".
- There is another method "predict_proba()".
- This method returns the probabilities for each class.
- The idea is that by changing the threshold to assign a record to class 1, we can control precision and recall.
- Let's check this using the undersampled data (best C_param = 0.01)
lr = LogisticRegression(C = 0.01, penalty = 'l1')
lr.fit(X_train_undersample,y_train_undersample.values.ravel())
y_pred_undersample_proba = lr.predict_proba(X_test_undersample.values)
thresholds = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]
plt.figure(figsize=(10,10))
j = 1
for i in thresholds:
y_test_predictions_high_recall = y_pred_undersample_proba[:,1] > i
plt.subplot(3,3,j)
j += 1
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test_undersample,y_test_predictions_high_recall)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
# Plot non-normalized confusion matrix
class_names = [0,1]
plot_confusion_matrix(cnf_matrix
, classes=class_names
, title='Threshold >= %s'%i)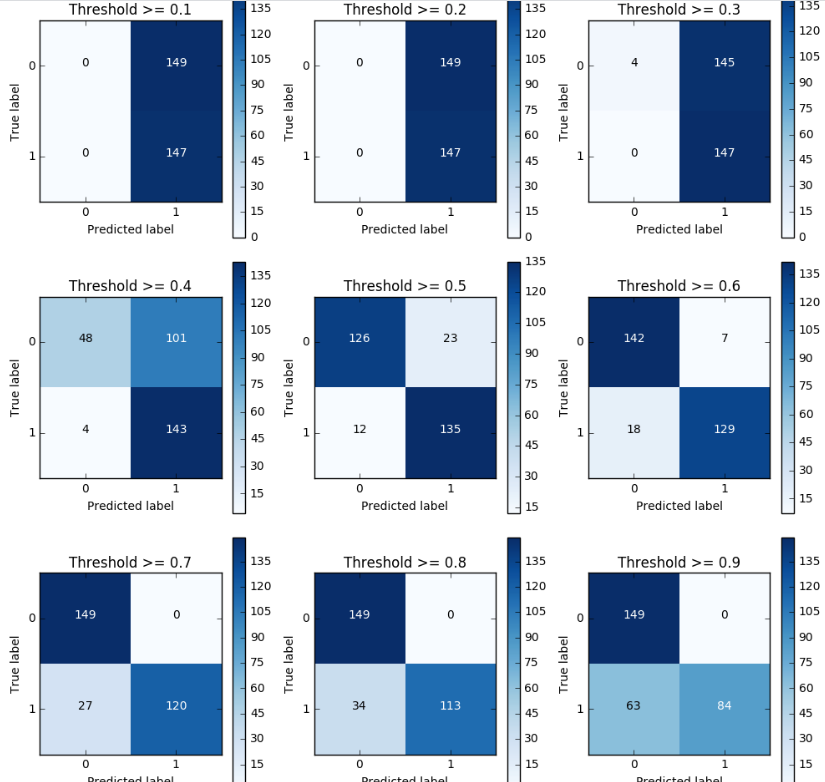
- The pattern is very clear: the more you lower the required probability to put a certain in the class "1" category, more records will be put in that bucket.
- This implies an increase in recall (we want all the "1"s), but at the same time, a decrease in precision (we misclassify many of the other class).
- Therefore, even though recall is our goal metric (do not miss a fraud transaction), we also want to keep the model being accurate as a whole.
- There is an option I think could be quite interesting to tackle this.
- We could assign cost to misclassifications, but being interested in classifying "1s" correctly, the cost for misclassifying "1s" should be bigger than "0" misclassifications.
- Incorrectly classifying an actual fraudulent transaction (1) as legitimate (0) (False Negative)
- This case should have a higher cost
- Incorrectly classifying a legitimate transaction (0) as fraudulent (1) (False Positive)
- This case should have a relatively lower cost
- After that, the algorithm would select the threshold which minimises the total cost.
- A drawback I see is that we have to manually select the weight of each cost... therefore, I will leave this know as a thought.
- Going back to the threshold changing, there is an option which is the Precision-Recall curve.
- By visually seeing the performance of the model depending on the threshold we choose, we can investigate a sweet spot where recall is high enough whilst keeping a high precision value.
9. Investigate Precision-Recall curve and area under this curve
from itertools import cycle
lr = LogisticRegression(C = 0.01, penalty = 'l1')
lr.fit(X_train_undersample,y_train_undersample.values.ravel())
y_pred_undersample_proba = lr.predict_proba(X_test_undersample.values)
thresholds = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]
colors = cycle(['navy', 'turquoise', 'darkorange', 'cornflowerblue', 'teal', 'red', 'yellow', 'green', 'blue','black'])
plt.figure(figsize=(5,5))
j = 1
for i,color in zip(thresholds,colors):
y_test_predictions_prob = y_pred_undersample_proba[:,1] > i
precision, recall, thresholds = precision_recall_curve(y_test_undersample,y_test_predictions_prob)
# Plot Precision-Recall curve
plt.plot(recall, precision, color=color,
label='Threshold: %s'%i)
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.ylim([0.0, 1.05])
plt.xlim([0.0, 1.0])
plt.title('Precision-Recall example')
plt.legend(loc="lower left")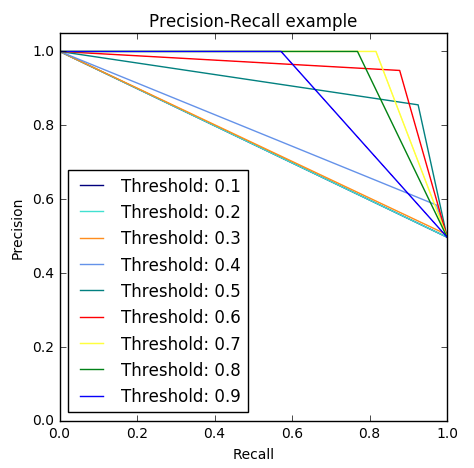
Second Kernel
- Disappeared.... :(
Third Kernel: Semi-Supervised Anomaly Detection Survey
- Explore some anomaly detection techniques.
Insight / Summary:
1. Three types of anomalies
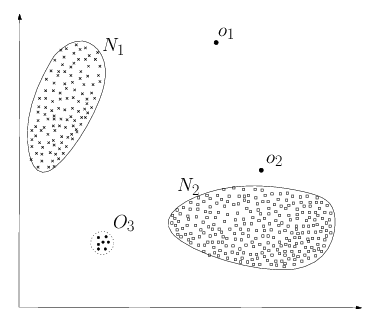
1) Point Anomaly
- "an individual data instance can be considered as anomalous with respect to the rest of data"
- In the image above, instance ( o_1 ) and ( o_2 ) and all instances in ( O_3 ) are point anomalies since they lie outside the normal regions.
- As another example, consider credit card transaction data, with information only about amount spent.
- Then, a high transaction compared to the rest for a particular individual is an anomaly.
2) Contextual Anomaly
- In this case, the data must have features regarding some contextual attribute (e.g. time, space) and some features regarding behavioral attributes.
- The anomaly is then determined within a given context.
- As an example, consider again credit card transactions, but now we have both information about the amount spend and day of the year.
- Now, a high amount transaction might be considered normal if it occurred in the week before Christmas, but the same amount transaction in July might be suspicious.
- We could also have information about the location the client is when performing transactions, and then expect high amounts if we detect he/she is somewhere far from home, as in a vacation.
3) Collective Anomaly
- In this case, some related data instances are anomalous with respect to the entire data set, but each individual instances may not be considered anomalous.
- As an example, consider the stock of a retailer.
- We expect to see its volume fluctuating in time, with low values followed by high values.
- However, a low stock for a long period of time is a anomaly.
- Note that the low volume per se is not an anomaly, but it persistence is.
2. Summary
- Note that the last two types assume some relation among data instances, that is, they are not independent identically distributed (i.i.d).
- In the present work, we have credit card transaction information and time is one of the features, so we could treat this problem as contextual anomaly detection.
- However, we only have two days of data, making it almost impossible to determine a useful temporal context.
- Hence, we will only consider point anomalies techniques to avoid the burden in the extra work of defining a context.
- Nonetheless, we will keep time as a feature, so in some sense the contextual information will be considered, although no directly modeled.
3. Challenges
- One straightforward approach to anomaly detection would be to simply define a region where the normal data lies and classify anything out of that region as an anomaly.
- This is most easily said than done and there are some major challenges that often arise in anomaly detection problem:
- Modeling a normal region that captures all normal behavior is extremely difficult and the boundary between normal an abnormal is often blurred.
- Anomalies might be the result of malicious actions. Then, the malicious adversaries are always trying to adapt to make anomalous observations seem normal.
- The normal behavior can change, and then a current notion of normal might not be valid in the future.
- As we've seen, the notion of an anomaly varies for different application domains, and there is no algorithm that can handle all of them equally well.
- Labeled data for training/validation of models used by anomaly detection techniques is usually a major issue, being either extremely scarce or non existent.
- If the data contains a lot of noise, it is difficult to distinguish noisy instances from anomalies.
4. Metric
- A system with high recall but low precision returns many results, but most of its predicted labels are incorrect when compared to the training labels.
- A system with high precision but low recall is just the opposite, returning very few results, but most of its predicted labels are correct when compared to the training labels.
- An ideal system with high precision and high recall will return many results, with all results labeled correctly.
- Since we are in a scenario of credit card fraud detection, failing to detect a fraud has a higher cost than assigning as fraudulent a normal transaction.
- Hence, we are more concerned with a high recall metric, as this shows that our system can consistently detect frauds, even if this means getting a few false positives.
- Nonetheless, we don't want to have a lot of false positives, since there is also a cost in verifying to much transactions assigned as frauds.
- So we can summarize our model's performance in a single metric, we will use the (( F_2 )) score, which places more importance in recall than precision. Formally, it is defined as:

5. Statistical Anomaly Detection Techniques
- We assume that Normal data instances occur in high probability regions of a stochastic model, while anomalies occur in the low probability regions of the stochastic model.
- In the statistical model techniques we fit a statistical model and perform statistical inference to decide if an unseen observation comes from the model distribution or not.
- One advantage of this methods is that we can associate a confidence interval to each prediction, which can help when deciding on a course of action to deal with the anomalies.
- Another advantages is that if the model is robust to anomalies, it can be used in an unsupervised fashion, without needing any labeled data.
1) Gaussian Model Based
from scipy.stats import multivariate_normal
mu = train.drop('Class', axis=1).mean(axis=0).values
sigma = train.drop('Class', axis=1).cov().values
model = multivariate_normal(cov=sigma, mean=mu, allow_singular=True)
print(np.median(model.logpdf(valid[valid['Class'] == 0].drop('Class', axis=1).values)))
print(np.median(model.logpdf(valid[valid['Class'] == 1].drop('Class', axis=1).values)))2) Histogram Based
class hist_model(object):
def __init__(self, bins=50):
self.bins = bins
def fit(self, X):
bin_hight, bin_edge = [], []
for var in X.T:
# get bins hight and interval
bh, bedge = np.histogram(var, bins=self.bins)
bin_hight.append(bh)
bin_edge.append(bedge)
self.bin_hight = np.array(bin_hight)
self.bin_edge = np.array(bin_edge)
def predict(self, X):
scores = []
for obs in X:
obs_score = []
for i, var in enumerate(obs):
# find wich bin obs is in
bin_num = (var > self.bin_edge[i]).argmin()-1
obs_score.append(self.bin_hight[i, bin_num]) # find bin hitght
scores.append(np.mean(obs_score))
return np.array(scores)
model = hist_model()
model.fit(train.drop('Class', axis=1).values)
print(np.median(model.predict(valid[valid['Class'] == 0].drop('Class', axis=1).values)))
print(np.median(model.predict(valid[valid['Class'] == 1].drop('Class', axis=1).values)))
6. Cluster based Technique
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=3, n_init=4, random_state=42)
gmm.fit(train.drop('Class', axis=1).values)
print(gmm.score(valid[valid['Class'] == 0].drop('Class', axis=1).values))
print(gmm.score(valid[valid['Class'] == 1].drop('Class', axis=1).values))
7. SVM based Technique
from sklearn.svm import OneClassSVM
np.random.seed(42)
model = OneClassSVM(gamma=0.000562, nu=.95, kernel='rbf')
model.fit(train.drop('Class', axis=1).values)
print(model.decision_function(valid[valid['Class'] == 0].drop('Class', axis=1).values).mean())
print(model.decision_function(valid[valid['Class'] == 1].drop('Class', axis=1).values).mean())
8. Tree based Technique
from sklearn.ensemble import IsolationForest
np.random.seed(42)
model = IsolationForest(random_state=42, n_jobs=4, max_samples=train.shape[0], bootstrap=True, n_estimators=50)
model.fit(train.drop('Class', axis=1).values)
print(model.decision_function(valid[valid['Class'] == 0].drop('Class', axis=1).values).mean())
print(model.decision_function(valid[valid['Class'] == 1].drop('Class', axis=1).values).mean())
9. Neural based Technique: AutoEncoder
Embrace challenges as opportunities for growth and transformation.
- Max Holloway -
'캐글' 카테고리의 다른 글
| [Kaggle Study] #14 Toxic Comment Classification Challenge (0) | 2024.12.04 |
|---|---|
| [Kaggle Study] #12 Spooky Author Identification (0) | 2024.12.04 |
| [Kaggle Study] #10 Zillow Prize: Zillow’s Home Value Prediction (Zestimate) (0) | 2024.11.29 |
| [Kaggle Study] #9 New York City Taxi Trip Duration (0) | 2024.11.29 |
| [Kaggle Study] #8 2018 Data Science Bowl (0) | 2024.11.28 |